Interface Summary
Interface	Description
FloatIAxis	An IAxis represents a binned histogram axis.
FloatIHistogram	A common base interface for IHistogram1D, IHistogram2D and IHistogram3D.
FloatIHistogram1D	A Java interface corresponding to the AIDA 1D Histogram.
FloatIHistogram2D	A Java interface corresponding to the AIDA 2D Histogram.
FloatIHistogram3D	A Java interface corresponding to the AIDA 3D Histogram.

Package hep.aida.tfloat Description

Interfaces for compact, extensible, modular and performant histogramming functionality.

Getting Started

1. Overview

Aida itself offers the histogramming features of HTL and HBOOK, the de-facto standard for histogramming for many years. It also offers a number of useful extensions, with an object-oriented approach. These features include the following:

creating and filling of 1D, 2D (and profile histograms, in the future)
computation of statistics such as the mean, rms, etc. of a histogram
support for operations between histograms (in the future)
browsing of and access to characteristics of individual histograms

File-based I/O can be achieved through the standard Java built-in serialization mechanism. All classes implement the Serializable interface. However, the toolkit is entirely decoupled from advanced I/O and visualisation techniques. It provides data structures and algorithms only.

This toolkit borrows many concepts from HBOOK and the CERN HTL package (C++) largely written by Savrak Sar.

The definition of an abstract histogram interface allows functionality that is provided by external packages, such as plotting or fitting, to be decoupled from the actual implementation of the histogram. This feature paves the way for co-existence of different histogram packages that conform to the abstract interface.

A reference implementation of the interfaces is provided by package hep.aida.tdouble.ref.

2. AIDA at a glance

Fixed-width histogram

The following code snippet demonstrates example usage:

 IHistogram1D h1 = new Histogram1D("my histo 1",10, -2, +2); // 10 bins, min=-2, max=2
 IHistogram2D h2 = new Histogram2D("my histo 2",10, -2, +2,    5, -2, +2);
 IHistogram2D h3 = new Histogram3D("my histo 3",10, -2, +2,    5, -2, +2,    3, -2, +2);

 // equivalent
 // IHistogram1D h1 = new Histogram1D("my histo 1",new FixedAxis(10, -2, +2)); 
 // IHistogram2D h2 = new Histogram2D("my histo 2",new FixedAxis(10, -2, +2),new FixedAxis(5, -2, +2));

 // your favourite distribution goes here
 cern.jet.random.AbstractDistribution gauss = new cern.jet.random.Normal(0,1,new cern.jet.random.engine.MersenneTwister());

 for (int i=0; i < 10000; i++) {    
    h1.fill(gauss.nextDouble());
    h2.fill(gauss.nextDouble(),gauss.nextDouble());
    h3.fill(gauss.nextDouble(),gauss.nextDouble(),gauss.nextDouble());
 }

 System.out.println(h1);
 System.out.println(h2);
 System.out.println(h3);
 rms=h1.rms();
 sum=h1.sumBinHeights();
 ...

Variable-width histogram

The following code snippet demonstrates example usage:

 double[] xedges = { -5, -1, 0, 1, 5 };
 double[] yedges = { -5, -1, 0.2, 0, 0.2, 1, 5 };
 double[] zedges = { -5, 0, 7 };
 IHistogram1D h1 = new Histogram1D("my histo 1",xedges); //
 IHistogram2D h2 = new Histogram2D("my histo 2",xedges,yedges);
 IHistogram2D h3 = new Histogram3D("my histo 3",xedges,yedges,zedges);

 // equivalent
 // IHistogram1D h1 = new Histogram1D("my histo 1",new VariableAxis(xedges)); 
 // IHistogram2D h2 = new Histogram2D("my histo 2",new VariableAxis(xedges),new VariableAxis(yedges));

 // your favourite distribution goes here
 cern.jet.random.AbstractDistribution gauss = new cern.jet.random.Normal(0,1,new cern.jet.random.engine.MersenneTwister());

 for (int i=0; i < 10000; i++) {    
    h1.fill(gauss.nextDouble());
    h2.fill(gauss.nextDouble(),gauss.nextDouble());
    h3.fill(gauss.nextDouble(),gauss.nextDouble(),gauss.nextDouble());
 }

 System.out.println(h1);
 System.out.println(h2);
 System.out.println(h3);
 rms=h1.rms();
 sum=h1.sumBinHeights();
 ...

Here are some example histograms, as rendered by Java Analysis Studio.

And here is an example output of DoubleConverter.toString(DoubleIHistogram2D).

my histo 2:
   Entries=5000, ExtraEntries=0
   MeanX=4.9838, RmsX=NaN
   MeanY=2.5304, RmsY=NaN
   xAxis: Bins=11, Min=0, Max=11
   yAxis: Bins=6, Min=0, Max=6
Heights:
      | X
      | 0   1   2   3   4   5   6   7   8   9   10  | Sum 
----------------------------------------------------------
Y 5   |  30  53  51  52  57  39  65  61  55  49  22 |  534
  4   |  43 106 112  96  92  94 107  98  98 110  47 | 1003
  3   |  39 134  87  93 102 103 110  90 114  98  51 | 1021
  2   |  44  81 113  96 101  86 109  83 111  93  42 |  959
  1   |  54  94 103  99 115  92  98  97 103  90  44 |  989
  0   |  24  54  52  44  42  56  46  47  56  53  20 |  494
----------------------------------------------------------
  Sum | 234 522 518 480 509 470 535 476 537 493 226 |

And here is a sample 3d histogram output.

3. Histograms

3.1 Axes

An axis (DoubleIAxis) describes how one dimension of the problem space is divided into intervals. Consider the case of a 10 bin histogram in the range [0,100]. An axis object containing the number of bins and the interval limits will describe completely how we divide such an interval: a set of 10 sub-intervals of equal width. This is termed a DoubleFixedAxis and can be constructed as follows

IAxis axis = new FixedAxis(10, 0.0, 100.0);

It may be required to work with an histogram over the same range as the example above, but with bins of variable widths. In this case, an axis containing the bin edges will describe completely how the interval [0,100] is divided. Such an axis is termed a DoubleVariableAxis and can be constructed as follows

double[] edges = { 0.0, 10.0, 40.0, 49.0, 50.0, 51.0, 60.0, 100.0 };
IAxis axis = new VariableAxis(edges);

An n-dimensional histogram thus contains n axes, one for each dimension. The only concern of an axis is to associate any ordered 1D space with a discrete numbered space. Thus it associates an interval to an integer. Hence, an axis knows about the width of the intervals and their lower point/bound or upper point/bound. An axis can be asked for such information as follows:

IAxis axis = new FixedAxis(2, 0.0, 20.0); // 2 bins, min=0, max=20
... 
axis.bins();          // Number of in-range bins (excluding underflow and overflow bins) 
axis.binLowerEdge(i); // and the lower edge of bin i
axis.binWidth(i);     // and its width
axis.binUpperEdge(i); // and its upper edge
double point = 1.23;
int binIndex = axis.coordToIndex(point); // Obtain index of bin the point falls into (maps to)

In this package, a histogram delegates to its axes the task of locating a bin. In other words, information about the lower and upper edges of a bin or the width of a given bin are obtained from the corresponding axis. This is shown in the following code fragment, which demonstrates how the lower and upper edges and width of a given bin can be obtained.

IHistogram1D histo = new Histogram1D("Histo1D", 10, 0.0, 100.0 ); 
... 
histo.xAxis().bins()           // Obtain the number of bins (excluding underflow and overflow bins)
histo.xAxis().binLowerEdge(i)  // and the lower edge of bin i
histo.xAxis().binWidth(i)      // and its width
histo.xAxis().binUpperEdge(i)  // and its upper edge

An axis always sucessfully maps any arbitrary point drawn from the universe [-infinity,+infinity] to a bin index, because it implicitly defines an additional underflow and overflow bin, both together called extra bins.

 IHistogram2D h = new Histogram2D(new FixedAxis(2, 0.0, 100.0), new FixedAxis(2, 0.0, 100.0), ...);

           y ^                          i ... in-range bin, e .. extra bins
             |                           
        +inf |                           
             |   e | e | e | e           
         100 -  ---------------
             |   e | i | i | e          --> in-range == [0,100]²
             |  ---------------         --> universe == [-infinity,+infinity]²
             |   e | i | i | e          --> extra bins == universe - inrange
           0 -  ---------------         
             |   e | e | e | e          
         -inf|  
              -----|-------|------> x
              -inf 0      100   +inf

For example if an axis is defined to be new FixedAxis(2, 0.0, 20.0), it has 2 in-range bins plus one for underflow and one for overflow. axis.bins()==2. Its boundaries are [Double.NEGATIVE_INFINITY,0.0), [0.0, 10.0), [10.0, 20.0), [20.0, Double.POSITIVE_INFINITY]. As a consequence point -5.0 maps to bin index IHistogram.UNDERFLOW, point 5.0 maps to bin index 0, 15.0 maps to bin index 1 and 25.0 maps to bin index IHistogram.OVERFLOW.

As a further example, consider the following case: new VariableAxis(new double[] { 10.0, 20.0 }). The axis has 1 in-range bin: axis.bins()==1. Its boundaries are [Double.NEGATIVE_INFINITY,10.0), [10.0, 20.0), [20.0, Double.POSITIVE_INFINITY]. Point 5.0 maps to bin index IHistogram.UNDERFLOW, point 15.0 maps to bin index 0 and 25.0 maps to bin index IHistogram.OVERFLOW.

As can be seen, underflow bins always have an index of IHistogram.UNDERFLOW, whereas overflow outlier bins always have an index of IHistogram.OVERFLOW.

3.2 Bins

Bins themselves contain information about the data filled into them. They can be asked for various descriptive statistical measures, such as the minimum, maximum, size, mean, rms, variance, etc.

Note that bins (of any kind) only know about their contents. They do not know where they are are located in the histogram to which they belong, nor about their widths or bounds - this information is stored in the axis to which they belong, which also defines the bin layout within a histogram.

4. Advanced Histogramming

TODO.

Comparison with the old AIDA interfaces

A proposed simpler alternative to the current hep.aida.flat classes.

The classes in this directory have been proposed by Mark Donselmann, Wolfgang Hoschek and Tony Johnson as a simpler, easier to use alternative to the classes orignally proposed as the AIDA standard.

Our goals were:

Eliminate methods that are primarily for developers writing display packages, they should not be complicating the public user interfaces.
Reduce unnecessary duplication which makes the interfaces very long without adding any additional functionality or ease-of-use
Eliminate methods that are hard to use (we could not think of any occasion where the 8 separate methods for getting the 2D overflows bins would be convenient for anyone).

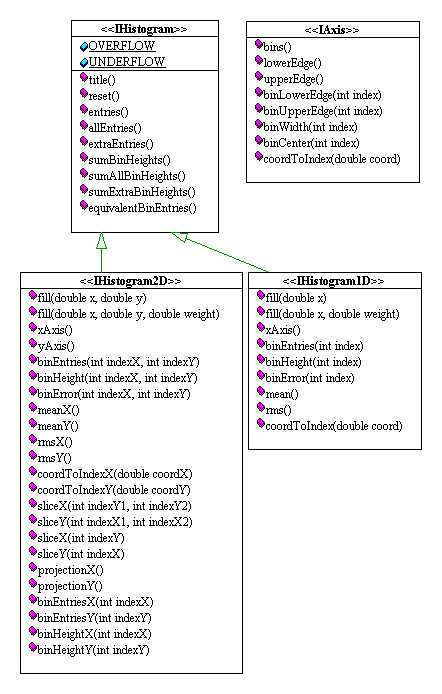
Note that ease of implementation was NOT a primary goal. Following these goals we were able to reduce the number of methods as follows:

OLD	# methods	NEW	#methods
IHistogram1D	45	IHistogram	9
IHistogram2D	89	IHistogram1D	9 (+ inherited from IHistogram)
		IHistogram2D	23(+9 inherited from IHistogram)
		Axis	8

The primary differences between the old classes and the new classes are:

Introduction of an IAxis class, to describe the X axis for 1D histograms, and the X and Y axes of 2D histograms. We understand that the desire is to keep the interfaces as flat as possible, but feel this introduces a significant improvement in terms of reducing complexity, and is an abstraction that is easy for even the most object-phobic physicist to grasp.
We define constants OVERFLOW and UNDERFLOW to represent the underflow and overflow bins on an axis. This eliminates the need for special routines that deal with overflows/underflows. It also improves the interface since it exposes the full set of overflow/underflow bins for 2D histograms. Under the previous proposal it was necessary for the implementation to keep the full set of overflow/underflow bins, in order to be able to do the projections correctly, but there was no way for the end-user to access them (they were restricted to the 8 overflow bins N,E,S,W,NE,SE,SW,NW).
We eliminated the methods which return information about bins based on coordinate (as opposed to index). We felt these functions were rarely used, were in some cases ambiguous (for example when projections/slices were specified in terms of coordinates what exactly was the meaning) and the same functionality with less ambiguity was available by calling coordToIndex() first.

A UML diagram of the classes is given below: