Net2Plan

Example: Capacity assignment minimizing network delay, with linear cost constraints

ca_minAvNetDelayLinearCost

This algorithm obtains the capacity assignment that minimizes the average network delay 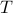in the network, so that the network cost is limited to a maximum budget $C_{max}$ .

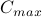Average network delay considers the queueing delay and the transmission delay. Propagation delay is not included since it is not affected by the link capacities. Average network delay 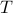is estimated as:

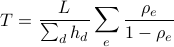
$T = frac{L}{sum_d h_d} sum_e frac{rho_e}{1 - rho_e}$

Where:

is the offered traffic in bps of demand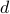
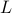: is the average packet length in bits
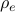: is the utilization of link

The network cost 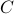is the sum of the costs of the links 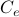C_e , where the cost in a link grows in a linear form respect to capacities:

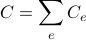
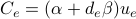
Where:

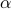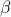, : are cost factors, input parameters to the problem.
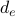: is the length in km of link
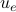: is the link capacity in Erlangs

The algorithm solves the following formulation:

Decision variables:

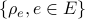: Utilization in the links

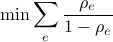
$min sum_e frac{rho_e}{1 - rho_e}$

$sum_e (alpha + d_e beta ) y_e frac{1}{rho_e} leq C_{max}$

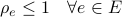
The previous formulation is a convex program respect to the 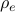rho_e variables, and is solved using CVX. The algorithm requires CVX solver installed and running.

Download .m file: ca_minAvNetDelayLinearCost.m