Net2Plan

Example: Capacity assignment minimizing maximum link utilization, with linear cost constraints

ca_minimaxUtilizationLinearCost

This algorithm obtains the capacity assignment that minimizes the maximum link utilization 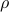rho in the network, so that the network cost is limited to a maximum budget $C_{max}$ .

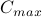The network cost 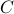is the sum of the costs of the links 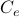C_e , where the cost in a link grows in a linear form respect to capacities:

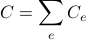
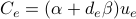
Where:

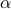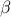, : are cost factors, input parameters to the problem.
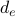: is the length in km of link
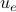: is the link capacity in Erlangs

The algorithm solves the following formulation:

Decision variables:

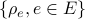: Utilization in the links
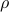: Maximum utilization in the links

$sum_e (alpha + d_e beta ) y_e frac{1}{rho_e} leq C_{max}$

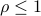
The previous formulation is a convex program respect to the 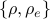lbrace rho, rho_e rbrace variables, and is solved using CVX. The algorithm requires CVX solver installed and running.

Download .m file: ca_minimaxUtilizationLinearCost.m