Net2Plan

Example: Routing that minimizes the average network delay, using flow-link formulation

fa_minNetDelay_xde

This algorithm obtains the traffic routing that minimizes the average network delay, using a convex flow-link formulation.

Average network delay considers the queueing delay, the transmission delay and the propagation delay. Average network delay 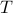is estimated as:

$T = frac{L}{sum_d h_d} sum_e frac{rho_e}{1 - rho_e} + frac{1}{sum_d h_d} y_e t_e$

Where:

is the offered traffic in bps of demand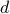
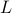: is the average packet length in bits
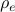: is the utilization of link
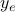: is the traffic in bps traversing link
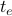: is the propagation delay in seconds for traversing link

The algorithm solves the following formulation:

Decision variables:

$lbrace x_{de}, d in D, e in E rbrace$ : Fraction of the traffic of demand 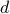that traverses link .
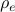: is the utilization of link

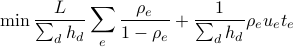
$min frac{L}{sum_d h_d} sum_e frac{rho_e}{1 - rho_e} + frac{1}{sum_d h_d} rho_e u_e t_e$

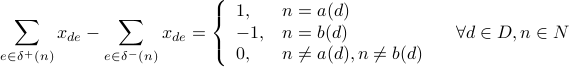
$sum_{e in delta^{+}(n)} x_{de} - sum_{e in delta^{-}(n)} x_{de} = left{ begin{array}{ll} 1, & n = a(d) -1, & n = b(d) 0, & n not = a(d), n not = b(d) end{array}right. quad forall d in D, n in N$

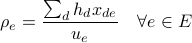
$rho_e = frac{sum_d h_d x_{de}}{u_e} quad forall e in E$

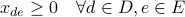
$x_{de} geq 0 quad forall d in D, e in E$

The previous formulation is a convex program respect to the decision variables, and is solved using CVX. The algorithm requires CVX solver installed and running.

Download .m file: fa_minNetDelay_xde.m