Net2Plan

Example: Routing minimizing maximum link utilization, using flow-path formulation

fa_minimaxUtilization_xdp

This algorithm obtains the traffic routing that minimizes the maximum link utilization, using a linear flow-path formulation. For each demand, the set of admissible paths is given by the 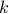loopless shortest paths between the demand end nodes. 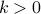k > 0 is an input parameter to the problem.

The algorithm first computes the list of admissible paths ( P_d, d in D ). Then, solves the following formulation:

Decision variables:

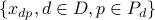$lbrace x_{dp}, d in D, p in P_d rbrace$ : Fraction of the traffic of demand 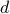that traverses the admissible path .
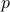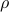: Maximum utilization in the links

$sum_{p in P_d} x_{dp} = 1 quad forall d in D$

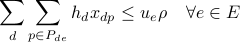
$sum_d sum_{p in P_{de}} h_d x_{dp} leq u_e rho quad forall e in E$

$x_{dp} geq 0 quad forall d in D, p in P_d$

In the previous formulation, the set 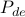$P_{de}$ is composed of the paths 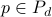p in P_d that traverse link . The previous formulation is a linear program respect to the decision variables, and is solved using CVX. The algorithm requires CVX solver installed and running.

Download .m file: fa_minimaxUtilization_xdp.m